지난 포스팅에서 시계열에 대해서 알아보았습니다.
2019/12/26 - [데이터 분석] - 시계열 분석 - 시계열 데이터란?
시계열 분석 - 시계열 데이터란?
1. 시계열 데이터 시계열 데이터는 '시간에 따라 관측된 자료'로 기후 데이터, 주가지수 등이 시간에 따라 변하는 시계열 데이터입니다. 시계열은 안정(stationary) 시계열과 불안정(non-stationary) 시계열 두..
domini21.tistory.com
이번 포스팅에서는 불안정 시계열을 안정 시계열로 변환하는 방법에 대해 알아보겠습니다.
- 로그(log) 변환
- 차분(diff)
파이썬 Random 함수를 이용해 시계열 자료를 만들고 증가추세를 임의 생성하였습니다.
import numpy as np
import pandas as pd
import matplotlib.pylab as plt
# 50개의 Random 시계열 생성
list_a = np.random.rand(50)
# idx만큼 증가하는 추세를 추가
list_a = [(idx+1) * val for idx, val in enumerate(list_a)]
plt.plot(list_a)
plt.show()

1. 로그변환
로그변환은 Numpy의 log 함수를 이용하여 변환하며 큰 값은 작게, 작은 값은 크게 조정됩니다.
# 로그함수
list_a = np.log(list_a)
plt.plot(list_a)
plt.show()
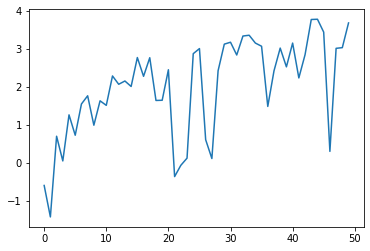
로그변환 데이터를 scale하였습니다. scale 후 Y축이 0값 전후로 데이터가 이동되었으나 추세는 남아있습니다.
from sklearn import preprocessing
list_a = preprocessing.scale(list_a)
plt.plot(list_a)
plt.show()
보통의 경우, 로그만으로는 안정시계열로 변환되진 않습니다.
로그함수를 취한 다음 차분(diff) 해야합니다.
2. 차분
차분은 현재시점($t_i$)의 자료에서 인접시점($t_{i-1}$)의 자료를 차감하는 것입니다.
예를 들어, 시계열 $\Delta Y$ = {1, 2, 3, 4, 5}를 1차 차분하면 $Y_t$에서 $Y_{t-1}$을 차감해야하므로,
차분한 시계열 $\Delta Y$ = {2-1, 3-2, 4-3, 5-4} = {1, 1, 1, 1} 이 됩니다.
import numpy as np
list_a = [1, 2, 3, 4, 5]
# Numpy의 diff 함수로 차분(1차 차분)
np.diff(list_a)
print(list_a) # 결과 : [1, 1, 1, 1]아래처럼 1차, 2차 차분을 적용할 수도 있으며, 차분은 추세가 제거되지만 데이터 손실이 발생합니다.
import numpy as np
list_a = [1, 3, 5, 7, 10]
# Numpy의 diff 함수로 차분(1차 차분)
list_a = np.diff(list_a, 1)
print(list_a) # 결과 : [2, 2, 2, 3]
# Numpy의 diff 함수로 차분(1차 차분)
list_a = np.diff(list_a, 2)
print(list_a) # 결과 : [0 1]다시, 시계열 데이터를 만들고 스케일 변환없이 로그변환과 차분을 해보겠습니다.
import numpy as np
import pandas as pd
import matplotlib.pylab as plt
# 시계열 자료를 만들고 추세를 추가
list_a = np.random.rand(50)
list_a = [(idx+1) * val for idx, val in enumerate(list_a)]
plt.plot(list_a)
plt.show()
# 로그변환
list_a = np.log(list_a)
plt.plot(list_a)
plt.show()
# 1차 차분
list_a = np.diff(list_a)
plt.plot(list_a)
plt.show()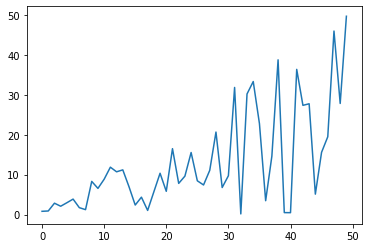


정상시계열로 변환된 것을 확인할 수 있습니다.
'데이터분석 > 시계열 분석' 카테고리의 다른 글
| 시계열 분석 - 시계열 데이터란? (4) | 2019.12.26 |
|---|

댓글