시계열 분석 - 시계열 데이터란?

1. 시계열 데이터 

시계열 데이터는 '시간에 따라 관측된 자료'로 기후 데이터, 주가지수 등이 시계열 데이터입니다.

시계열자료 예시 - 주가지수

시계열자료 예시 - 날씨

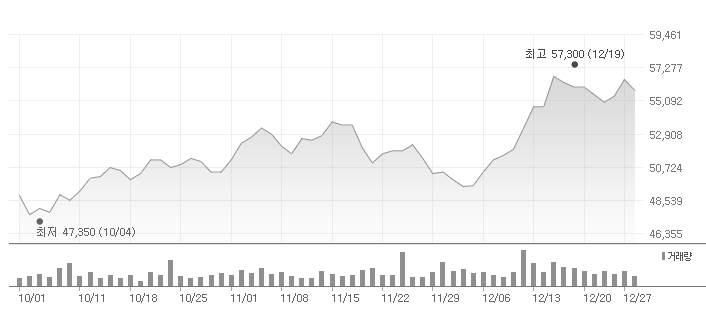
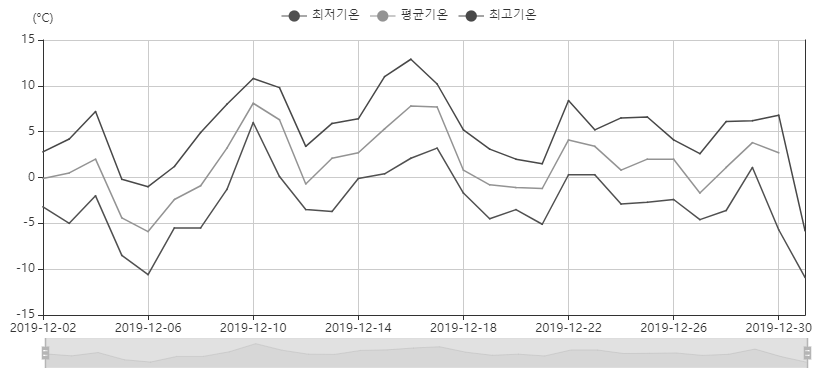
시계열 데이터는 데이터의 중심값과 산포(흩어진 정도)를 확인합니다.

히스토그램, 확률밀도함수를 그려서 확인 할 수 있으며, 파이썬에서는 Pandas의 describe() 함수로도 확인이 가능합니다. 

 

데이터의 산포는 중심으로부터 어느정도 흩어져있는지 파악하는 것으로 분산, 표준편차, 사분위수로 확인합니다.

• 분산
• 표준편차
• 사분위수

히스토그램(Histogram)

 

시계열의 중심척도를 알아볼 수 있는 요소로는 평균, 중앙값, 최빈값 등이 있습니다.

평균(average)은 데이터 합의 중심을, 중앙값(mean)은 크기 순으로 나열했을 때 중앙 위치의 값을 나타냅니다.

 

• 평균
• 중앙값
• 최빈값

---

시계열은 안정(stationary) 시계열과 불안정(non-stationary) 시계열 두 가지로 구분되는데, 안정 시계열은 데이터의 어떤 구간에서도 평균값과 분산(데이터의 흩어짐 정도)이 일정한 경우를 말합니다. 이를 정상 시계열이라고도 합니다.

 

• 안정 시계열 = 정상 시계열
• 불안정 시계열 = 비정상 시계열

아래 시계열 자료에서 빨간색과 푸른색 부분의 평균, 분산은 모두 다릅니다.

이런 경우가 비정상 시계열이구요.

아래처럼 평균은 거의 같지만, 분산이 다른 케이스도 비정상 시계열입니다.

 

정상 시계열은 아래와 같이 어느 구간에서도 평균과 분산이 거의 같아야 합니다.

그렇다면 왜 시계열 분석을 위해서 안정 시계열로 변환해야 하는 걸까요?

 

시계열 분석을 위해서는 시계열 모형을 만들어야 합니다. 자료는 우리가 관측한 데이터(우리가 알고있는)이고 모형은 이론적이지만 실제가 아닌 데이터(우리가 모르는)입니다. 우리가 모르는 시계열 모형을 만들기 위해서는 데이터의 값이나 확률분포를 수치화해야하는데 데이터의 추세(trend), 계절성(seasonality)이 있으면 시간에 따라 값이나 확률분포의 의미가 달랍니다.

 

따라서 시계열 분석의 일반적인 경우는 추세, 계절성을 제거해서 분석해야 합니다.

 

AR, MA, ARMA, ARIMA 등 통계적 모델은 과거의 N 시점의 값을 선형회귀에 대한 입력으로 사용하여 N+1을 예측하는 일종의 회귀모형입니다. 따라서 확률분포와 같은 통계 값이 시간에 따라 변하지 않아야 합니다.

 

다만, RNN, LSTM 과 같은 인공지능 모델은 비선형적 모델이라고 할 수 있기때문에 안정시계열로 변환할 필요가 없습니다.

 

2. 안정 시계열 변환

불안정 시계열을 안정시계열로 변환하려면 일반적으로 시계열 자료를 차분(diff)해야 합니다. 안정시계열 변환 방법과 파이썬 예제는 다음 게시글을 참고하시길 바랍니다.

2020/01/01 - [데이터 분석/시계열 분석] - 시계열 분석 - 안정(정상) 시계열로 변환

시계열 분석 - 안정(정상) 시계열로 변환